Dovendo calcolare la distanza fra due punti GPS, ho cercato su DuckDuck un aiuto per poter eseguire il calcolo ed ho adattato quello trovato facendolo divenire il seguente pezzo di codice PHP:
function distanza(lat2,lon2)
{
$R=6371;
$pigreco=3.1415927;
$f=0;
$p=0;
$d1=0;
// Coordinate di Piazza del Campidoglio, Roma
$lat2=41.89326;
$lon2=12.48298;
/* Converte i gradi in radianti */
$lat_alfa = $pigreco * $lat1 / 180;
$lat_beta = $pigreco * $lat2 / 180;
$lon_alfa = $pigreco * $lon1 / 180;
$lon_beta = $pigreco * $lon2 / 180;
// Calcola l’angolo compreso fi
$fi = abs($lon_alfa – $lon_beta);
// Calcola il terzo lato del triangolo sferico
$p = acos(sin($lat_beta) * sin($lat_alfa) + cos($lat_beta) * cos($lat_alfa) * cos($fi));
// Calcola la distanza sulla superficie terrestre R = ~6371 km
$d1 = $p * $R;
}
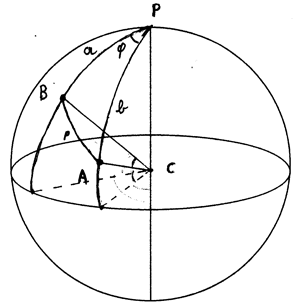
Non servendomi una grande precisione, assumo che la terra sia una sfera perfetta .
Dunque, osservando la figura in alto, diciamo che, in base alla trigonometria sferica (teorema di Eulero), tra i lati a, b e p del triangolo sferico ABP vale la relazione:
cos p = cos a cos b + sen a sen b cos φ
Ora, dette lat(A), lon(A), lat(B), lon(B), la latitudine e la longitudine dei punti A e B e, considerato che utilizzando la regola mnemonica di Nepero si ha:
- a = 90° – lat(B)
- b = 90° – lat(A)
- φ = lon(A) – lon(B)
abbiamo tutti i dati per calcolare la lunghezza del lato p considerando il raggio della Terra approssimabile a R = 6371 km.
